所谓递归,简单来说就是在函数内部调用函数自身。
我们常见到的计算阶乘、斐波那契数列就可以使用递归来完成。
递归需要程序在执行过程中不断调用自身,当然也必须要有一个明确的结束条件,不然就停不下来了。现在就简单的实现一下递归的阶乘:
1
2
3
4
5
function factorial(n){
if (n <= 1)
return 1;
return n * factorial(n - 1);
}
使用三目运算符优化一下代码:
1
2
3
function factorial(n) {
return n <= 1 ? 1 : n * factorial(n - 1);
}
这个示例中,当满足 n <= 1 这个条件时,固定返回数值 1,这就是递归过程中的明确结束条件。
对于计算阶乘的递归来说,由于其每次仅仅递归调用自身一次,所以不会引起较大的问题,但是对于一些相对复杂的递归,可能就会出现较大的问题,做一些技巧性的缓存还是很有必要的。比如递归最经典的使用场景就是计算斐波那契数列,但是每次调用过程中会在此调用自身函数两次,于是乎,2变4,4变8,量级成2的指数级增长,当计算一些稍大的数时,便会大大增加运行时间,或者有可能导致栈溢出。
计算斐波那契数列的递归调用如下:
1
2
3
function fibonacci(n){
return (n <= 2) ? 1 : fibonacci(n - 1) + fibonacci(n - 2);
}
下面我们写个测试函数,来看看求斐波那契数列某项时的耗时:
1
2
3
4
5
function t(n){
console.time("a");
console.log(fibonacci(n));
console.timeEnd("a");
}
(说明:当需要统计一段代码的执行时间时,可以使用console.time() 方法与console.timeEnd() 方法,其中console.time() 方法用于标记开始时间,console.timeEnd() 方法用于标记结束时间,并且将结束时间与开始时间之间经过的毫秒数在控制台中输出。这两个方法均使用一个参数,参数值可以为任何字符串,表示计时的 id,但是这两个方法所使用的参数字符串必须相同,才能正确地统计出开始时间与结束时间之间所经过的毫秒数。)
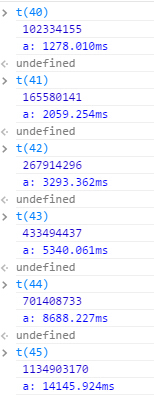
当数列项较小时,所消耗时间还不是非常多,上图为测试第40项开始的几条数据,我们看到,数列每增加一项,求解时所消耗的时间增加越多,到第45项时,已经要消耗 14 秒多的时间了。
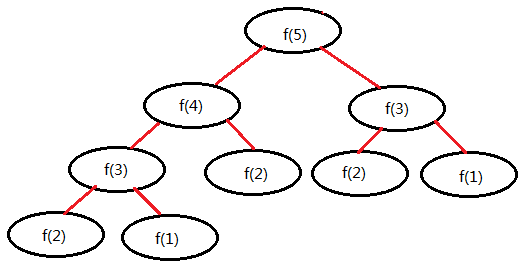
我们可以再通过以下图示来看一下,当计算第 5 项时函数调用的次数:
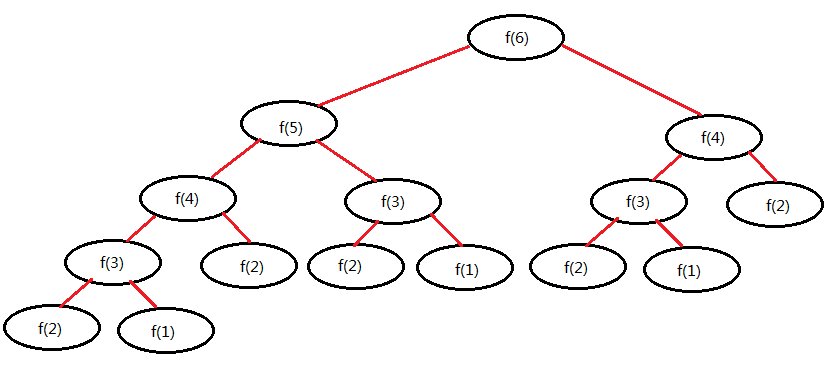
当计算第 6 项时函数调用的次数:
当计算第 7 项时函数调用的次数:
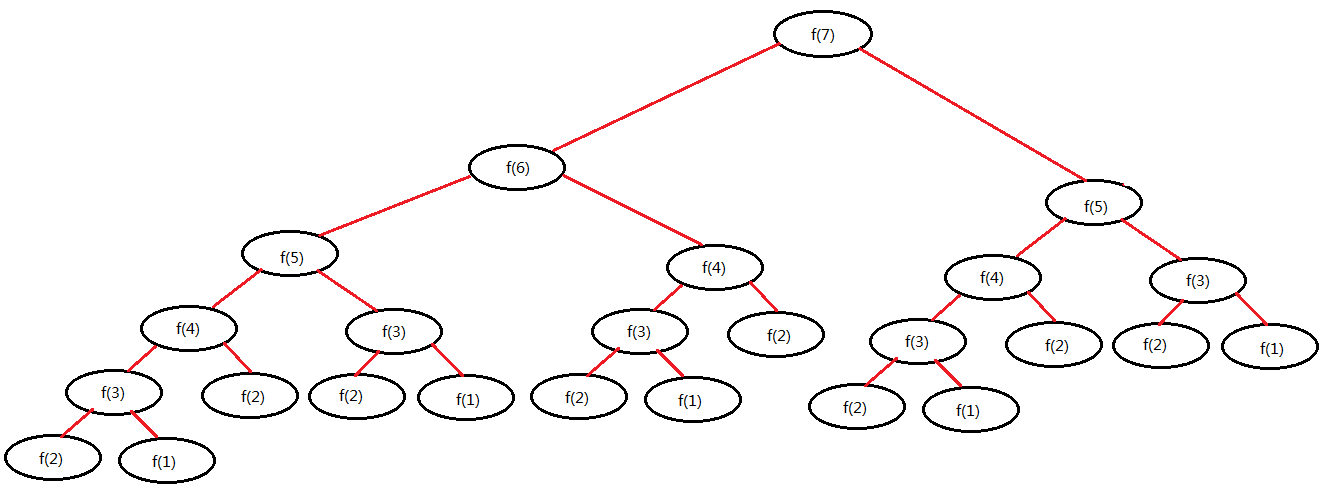
可以看出,每增加 1 项的计算,并不会只是增加 1 次函数的调用,而是会增加重复的多次函数调用,由此可见,递归调用在时间开销上是比较大的,这时,我们可以使用缓存方式来优化一下:
1
2
3
4
var fibArr = [undefined, 1, 1];
function fibonacci( n ){
return fibArr[n] ? fibArr[n] : (fibArr[n] = fibonacci(n - 1) + fibonacci(n - 2));
}
这时我们再看测试结果:
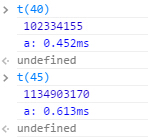
我们将斐波那契数的计算量级从 2 的指数次级,降到了常量 n 次级,并且由于缓存,在多次运行将量级降得更低,并且该方法也很好的缓解了栈溢出问题。
循环和递归的方法通常可以互相转换。任何一个循环的代码都可以用递归改写,实现相同的功能;反之亦然。所以我们也可以作如下修改:
1
2
3
4
5
6
7
8
9
10
function fibonacci( n ){
var first = 1, fib = 1, i = 2, tmp;
while( i < n ){
tmp = fib;
fib = first + fib;
first = tmp;
i++;
}
return fib;
}
测试:
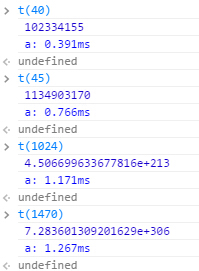
哇哦~~~~~~
我们将递归改为循环后,其实他的量级与优化后带缓存的递归是类似的,不过循环的量仅仅是计算,而递归的每个量都是调用一次函数,这也是两者最大的差别。